Impact of Funding and Funding Rounds on Startups Growth
In this project we apply Independent Two Sample T-Test and Chi-Square Test to assess the impact of funding and funding rounds on startups in India.
Table of contents
- 00. Project Overview
- 01. Concept Overview
- 02. Data Overview & Preparation
- 03. Applying Data Cleaning & EDA
- 04. Applying Two Sample Independent T-Test
- 05. Applying Chi-Square Test For Independence
- 05. Conclusion
- 06. Growth & Next Steps
Project Overview
Context
Company X, a leading Indian online publisher dedicated to startup industry insights, is driven by a mission to empower its audience with actionable knowledge. In the dynamic world of startups, the company recognizes the crucial need to answer a pivotal question: What financial factors differentiate thriving, currently operating startups from those that ultimately cease operations?
This project seeks to address the critical questions of whether there is a statistically significant difference in the mean funds raised by startups that are currently operating compared to those that have ceased operations. Additionally, we aim to investigate whether there exists a significant disparity in the number of funding rounds between currently operating startups and startups that have closed.
Actions
We removed incorrect or irrelevant values from the dataset & formatted it for proper analysis. Based on the problem statements, we filtered the data aka the variables of our interest such as funding_total_usd, status and funding_rounds.
For the problem mean funds raised by startups, we applied the Independent Two Sample T-test because the two groups aka ‘operating’ & ‘closed’ startups are separate and independent. Also we used levene’s test, a key assumption to determine whether the variance of the two sample groups are same or not. The results turned out to be positive that the variance of the sample means are equal, thus meeting the assumption for the independent sample t-test.
We set out our hypotheses and Acceptance Criteria for the test, as follows:
- Null Hypothesis: There is no statistically significant difference in the mean funds raised by currently operating startups and startups that have closed. They are independent.
- Alternate Hypothesis: There is a statistically significant difference in the mean funds raised by currently operating startups and startups that have closed. They are not independent.
- Acceptance Criteria: 0.05
We fed this into the algorithm (using the scipy library) to calculate the T-Statistic, p-value.
For the problem number of funding rounds for startups, As it is focused on comparing the funding rounds of two groups aka ‘operating’ & ‘closed’ startups - we applied the Chi-Square Test For Independence. Full details of this test can be found in the dedicated section below.
Note: Another option when comparing “funding rounds” is a test known as the Z-Test For Proportions. While, we could absolutely use this test here, we have chosen the Chi-Square Test For Independence because:
- The resulting test statistic for both tests will be the same
- The Chi-Square Test can be represented using 2x2 tables of data - meaning it can be easier to explain to stakeholders
- The Chi-Square Test can extend out to more than 2 groups - meaning the client can have one consistent approach to measuring signficance
We isolated startups data that are “Operating” and “Closed”.
We set out our hypotheses and Acceptance Criteria for the test, as follows:
- Null Hypothesis: There is no statistically significant difference in the number of funding rounds between currently operating startups and startups that have closed. They are independent.
- Alternate Hypothesis: There is a statistically significant difference in the number of funding rounds between currently operating startups and startups that have closed. They are not independent.
- Acceptance Criteria: 0.05
As a requirement of the Chi-Square Test For Independence, we aggregated this data down to a 2x2 matrix for rounds of funding category by status and fed this into the algorithm (using the scipy library) to calculate the Chi-Square Statistic, p-value, Degrees of Freedom, and expected values.
Results
Independent Two Sample T-Test gives us the following statistics:
- p-value: 0.5429592211146083
The p-value for our specified acceptance criteria or alpha of 0.05 is 0.54.
Based upon these statistics, we retain the null hypothesis, and conclude that There is no relationship between the mean funds raised by the two groups i.e. startups which are operating & startups. They are independent.
The Chi-Square Test gives us the following statistics:
- p-value: 0.2908506204110049
The p-value for our specified acceptance criteria or alpha of 0.05 is 0.29.
Based upon the above statistics, we retain the null hypothesis, and conclude that: There is no relationship in the number of funding rounds between currently operating startups and startups that have closed. They are independent.
Growth/Next Steps
Due to probabilistic nature of the hypothesis testing, Our results here also do not say that there definitely isn’t a difference in the mean funds/number of funding rounds between the two status groups aka ‘operating’ & ‘closed - we are only advising that we should not make any rigid conclusions at this point.
Running more tests like this, gathering more data, and then re-running this test may provide us, and the client more insight!
Concept Overview
Hypothesis Testing
Hypothesis refers to a statement or assumption about a population parameter, which is a characteristic of a larger group or population. A Hypothesis Test is used to assess the plausibility, or likelihood of an assumed viewpoint based on sample data - in other words, a it helps us assess whether a certain view we have about some data is likely to be true or not.
The objective of the Hypothesis Testing is to ESTABLISH a specific value for the parameter(s) and perform a statistical TEST to see whether that value is tenable(meaning - defensible or justifiable) in the light of the evidence gathered from the sample.
The Null Hypothesis
Null hypothesis(Ho) - the presumed current status of the matter or status quo. It is a statement assumed to be true if proven otherwise.
In any Hypothesis Test, we start with the Null Hypothesis. The Null Hypothesis is where we state our initial viewpoint, and in statistics, and specifically Hypothesis Testing, our initial viewpoint is always that the result is purely by chance or that there is no relationship or association between two outcomes or groups.
The Alternate Hypothesis
Alternative hypothesis(Ha) - It represents the opposing viewpoint, a specific research hypothesis or a targeted improvement basically something that challenges null hypothesis.
The aim of the Hypothesis Test is to look for evidence to support or reject the Null Hypothesis. If we reject the Null Hypothesis, that would mean we’d be supporting the Alternate Hypothesis. The Alternate Hypothesis is essentially the opposite viewpoint to the Null Hypothesis - that the result is not by chance, or that there is a relationship between two outcomes or groups.
What is one tailed test?
One-Tailed test talks about only one direction. Direction can be “Increase” or “Decrease” but not both.
For example, The Research question: Does a new exercise regimen lead to an increase in average running speed?
- Null Hypothesis(H0): The new exercise regimen does not result in an increase in average running speed.
- Alternative hypothesis(Ha): The new exercise regimen leads to a significant increase in average running speed.
What is two tailed test?
Two-Tailed test talks about both directions. This is why it is called Two-tailed t-test
For example, The Research question: Is the average IQ score of a sample significantly different from the national average of 100 ?
- Null Hypothesis(H0): The average IQ score of the sample is not significantly different from the national average of 100.
- Alternative Hypothesis(Ha): The average IQ score of the sample is significantly different from the national average of 100.
What is Test Statistic
- A test statisitc is a numerical value calculated from sample data during hypothesis testing
- It serves as a way to quantify the difference between the sample data and the expected values under the null hypothesis
- In Simpler terms, a test statistic helps us decide whether the observed data supports or contradicts the null hypothesis.
- If the test statistic is far from what would be expected under the null hypothesis, it suggests favor towards alternative hypothesis.
- Different types of tests and statistical methods have their own specific test statistics
- For example, in a t-test, the test statistic is the t-value, while in a chi-square test, it’s the chi-square statistic
- The choice of test statistic depends on the nature of the data and the specific hypothesis being tested
probabilistic nature of hypothesis testing
- The very nature of hypothesis testing is that it is probabilistic in nature. We say this because hypothesis testing relies on using a sample of data to make conclusions about an entire population.
- Imagine you’re trying to figure out the average height of all students in a huge school, but its impossible to measure everyone. So you measure a smaller group. your “sample”.
- Now, because you’re working with a sample, your conclusions aren’t 100% certain.
- They’re educated guesses based on probability. Just like you can’t be sure that a coin will land heads up every time you flip it. you can’t be certain about your conclusions in hypothesis testing.
- It’s about making the best guess, knowing that there’s a chance you might not be completely right due to the limited sample you’re using.
- As our conclusions in hypothesis testing are not 100% certain and because of this only there is an element of chance or probability that is involved and we must be extremely careful.
- Sometimes our result may not be right thing and that’s the reason there are errors associated with hypothesis testing.
Type I and Type II Error
As the results/conlusions in hypothesis testing are not 100% certain, there are errors associated with hypothesis testing.
- As previously demonstrated, the process of testing hypothesis is inherently susceptible to errors
- Null Hypothesis: The new drug has no effect on blood pressure.
- Alternate Hypothesis: The new drug lowers blood pressure.
- Type I Error ( false positive ): “ The new drug has no effect on blood pressure, but the study incorrectly concludes that it does”.
- Type II Error ( false negative ): “ The new drug lowers blood pressure, but the study fails to detect this effect “
Level of Significance, p-value, critical region
- Level of Significance: Probability of rejecting the null hypothesis when it is true. Let us set it at 5%
- Acceptance or Rejection Region: The total area under the distribution curve of the test statistic is partitioned into acceptance and rejection region. Reject the null hypothesis when the test statistic lies in the rejection region, Else we fail to reject it.
- P-value: Probability of observing test statistic or more extreme results than the computed test statistic, under the null hypothesis. p-value depends on the value of test statistic.
There are two ways to compare the final answer of hypothesis testing, one way to get the answer is looking at the p-value and the level of significance and other way is to look at the test statistic and the critical value.
Types Of Hypothesis Test
There are many different types of Hypothesis Tests, each of which is appropriate for use in differing scenarios - depending on a) the type of data that you’re looking to test and b) the question that you’re asking of that data.
In the case of our task here, where we are looking to understand the impact of funding and funding rounds on startups in India - We will utilise the Independence Two sample T-Test and Chi-Square Test For Independence.
Independent Two Sample T-Test
When we want to compare means from 2 samples that are independent, we then use Independent two sample t-test. The assumption of two sample t-test is that the variance of the samples should be same. We need to make sure that this assumption is satisfied and to test this assumption there is a test called levene’s test.
Chi-Square Test For Independence
The Chi-Square Test For Independence is a type of Hypothesis Test that assumes observed frequencies for categorical variables will match the expected frequencies.
The assumption is the Null Hypothesis, which as discussed above is always the viewpoint that the two groups will be equal. With the Chi-Square Test For Independence we look to calculate a statistic which, based on the specified Acceptance Criteria will mean we either reject or support this initial assumption.
The observed frequencies are the true values that we’ve seen.
The expected frequencies are essentially what we would expect to see based on all of the data.
Data Overview & Preparation
The data set contains information on all the startups in India
In the code below, we:
- Load in the Python libraries we require for importing the data
- Import the required data
# import library
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
%matplotlib inline
# import dataset
startup_df = pd.read_excel(r"/Users/praju/Desktop/Intensive_bootcamp/Statistics_for_Data_Analysis_level_2/Startup_Project/Funding_dataset.xlsx")
startup_df.head()
A sample of this data (the first 5 rows) can be seen below:
| permalink | name | homepage_url | category_list | funding_total_usd | Status | Country_Code |
|---|---|---|---|---|---|---|
| /organization/-fame | #fame | http://livfame.com | Media | 10000000.0 | operating | IND |
| /organization/21diamonds-india | 21Diamonds | http://www.21diamonds.de | E-Commerce | 6369507.0 | operating | IND |
| /organization/247-learning-private | 24x7 Learning | http://www.24x7learning.com | EdTech Education Systems | 4000000.0 | operating | IND |
| /organization/33coupons | 33Coupons | http://33coupons.in | Internet | 20000.0 | operating | IND |
| /organization/3dsoc | 3DSoC | http://www.3dsoc.com | 3D Mobile | 2065000.0 | operating | IND |
| State_Code | Region | City | Funding_Rounds | Founded_At | First_Funding_At | Last_Funding_At |
|---|---|---|---|---|---|---|
| 16.0 | Mumbai | Mumbai | 1 | NaT | 2015-01-05 | 2015-01-05 |
| 10.0 | New Delhi | Gurgaon | 1 | 2012-06-01 | 2012-11-15 | 2012-11-15 |
| 19.0 | Bangalore | Bangalore | 1 | 2001-01-01 | 2007-11-06 | 2007-11-06 |
| 36.0 | Kanpur | Kanpur | 1 | 2015-05-01 | 2015-07-06 | 2015-07-06 |
| 19.0 | Bangalore | Bangalore | 2 | 2006-06-01 | 2007-12-01 | 2010-08-01 |
Data Dictionary:
- Permalink - Refers to the link to the organisation.
- name - Company Name.
- homepage_url - Startup site.
- Category_list - Field of the company.
- Funding_Total_USD - Total fundings in USD.
- Status - Company’s status whether it is operating or closed.
- Country_Code - Refers the code for each country.
- State_Code - State code of the company location.
- Region - Region of the company location.
- City - City of company location.
- Funding_Rounds - Number of funding rounds for each company.
- Founded_At - Refers to the origin of the company.
- First_Funding_At - Refers to the date where first funding took place.
- Last_Funding_At - Refers to the date where last funding took place.
Applying Data Cleaning & EDA
We dive into the dataset, conducting a thorough examination to ensure its quality and coherence, while also gaining a deeper understanding of the data.
Checking Shape and Duplicate rows
# checking shape of the dataset
startup_df.shape
>> (1536, 14)
# Check for duplicate rows
startup_df.drop_duplicates().shape
>> (1536, 14)
There are no duplicates in the data.
Checking null values of variables
# Assuming startup_df is your DataFrame
columns_to_check = ['status', 'funding_total_usd', 'funding_rounds']
# Check for null values in the specified columns
null_counts = startup_df[columns_to_check].isnull().sum()
# Display the null value counts for each column
print(null_counts)
Output:
| status | 0 |
| funding_total_usd | 0 |
| funding_rounds | 0 |
There is no null value in the variables of our interest.
Checking Information of the Dataset.
startup_df.info()
Output:
| Column | Non-Null Count | Dtype |
|---|---|---|
| permalink | 1536 non-null | object |
| name | 1536 non-null | object |
| homepage_url | 1510 non-null | object |
| category_list | 1493 non-null | object |
| funding_total_usd | 1536 non-null | object |
| status | 1536 non-null | object |
| country_code | 1536 non-null | object |
| state_code | 1520 non-null | float64 |
| region | 1516 non-null | object |
| city | 1516 non-null | object |
| funding_rounds | 1536 non-null | int64 |
| founded_at | 1255 non-null | datetime64[ns] |
| first_funding_at | 1536 non-null | datetime64[ns] |
| last_funding_at | 1536 non-null | datetime64[ns] |
There are no null or duplicate values in the dataset but we could see that the total_funding_usd column should be cleaned and the datatype should be formatted.
Dropping Incorrect data in ‘funding_total_usd’ column
#Dropping "-" in funding_total_usd column and resetting the index values
startup_df = startup_df[startup_df['funding_total_usd']!='-']
startup_df.reset_index(drop = True)
startup_df.shape
>> (1134, 14)
Formatting the column ‘funding_total_usd’ & Checking Info of the dataset
#Dropping "-" in funding_total_usd column and resetting the index values
startup_df = startup_df[startup_df['funding_total_usd']!='-']
startup_df.reset_index(drop = True)
startup_df.shape
>> (1134, 14)
startup_df.info()
Output:
| Column | Non-Null Count | Dtype |
|---|---|---|
| permalink | 1134 non-null | object |
| name | 1134 non-null | object |
| homepage_url | 1113 non-null | object |
| category_list | 1115 non-null | object |
| funding_total_usd | 1134 non-null | float64 |
| status | 1134 non-null | object |
| country_code | 1134 non-null | object |
| state_code | 1125 non-null | float64 |
| region | 1122 non-null | object |
| city | 1122 non-null | object |
| funding_rounds | 1134 non-null | int64 |
| founded_at | 940 non-null | datetime64[ns] |
| first_funding_at | 1134 non-null | datetime64[ns] |
| last_funding_at | 1134 non-null | datetime64[ns] |
Checking value counts of column ‘status’
status_counts = startup_df['status'].value_counts()
status_counts
Output:
| operating | 1085 |
| closed | 49 |
Visualising ‘status’ column
# Visualize 'Status' column
status_counts = startup_df['status'].value_counts()
# Plotting
plt.figure(figsize=(8, 6))
plt.bar(status_counts.index, status_counts.values, color='blue')
plt.xlabel('Startup Status')
plt.ylabel('Count')
plt.title('Distribution of Startup Status')
# Adding data labels (count values) to the bars
for i, v in enumerate(status_counts):
plt.text(i, v + 10, v, ha='center')
# i: This is the x-coordinate where the data label will be placed.
# v + 10: This is the y-coordinate where the data label will be placed
# ha='center': This parameter specifies the horizontal alignment of the text, ensuring that it's centered above each bar.
# Display the plot
plt.show()
Above code gives us the below plot - which visualises our results!
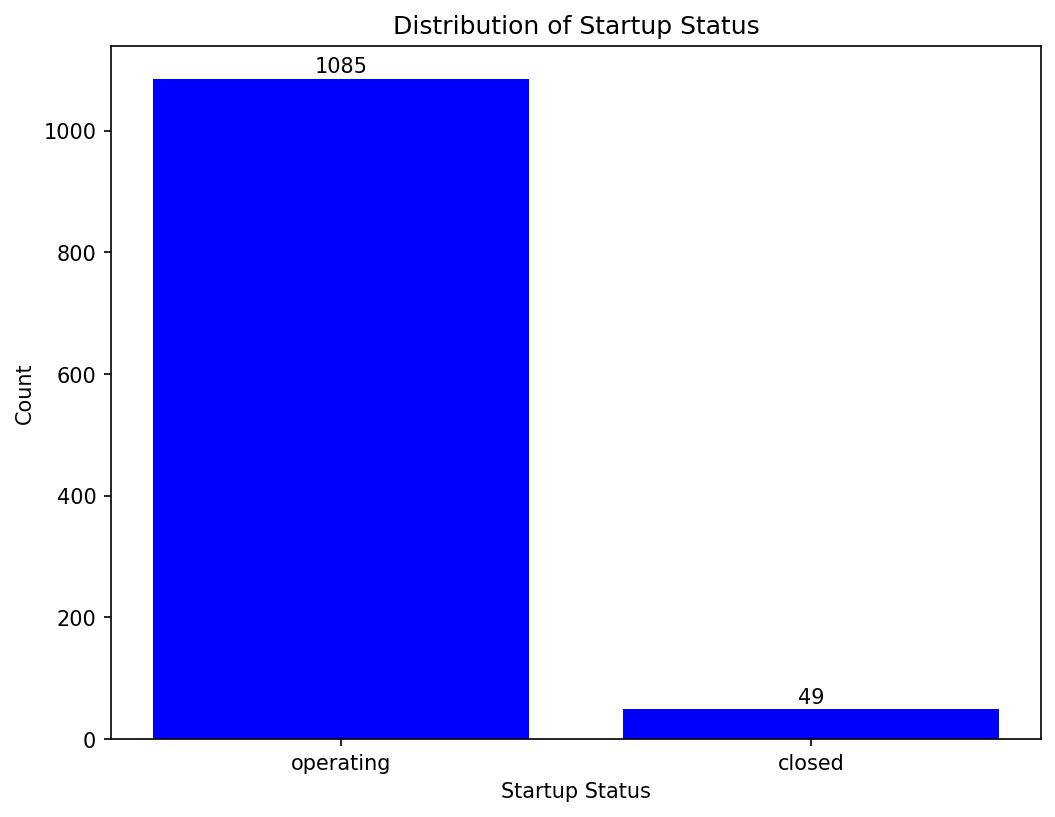
The dataset is imbalanced aka there are 1085 companies operating and 49 companies closed.
Inspecting ‘Funding’ column
# Let us understand more about funding column
# Set the display format for float numbers to display complete numbers
pd.options.display.float_format = '{:.0f}'.format
# By setting pd.options.display.float_format to ' {:.0f}'.format, you instruct pandas to format floating-point numbers with
# zero decimal places, effectively displaying complete numbers.
# Assuming startup_df is your DataFrame
description = startup_df['funding_total_usd'].describe()
# Display the description with complete numbers
print(description)
Output:
| count | 1134 |
| mean | 23391193 |
| std | 153640842 |
| min | 569 |
| 25% | 200000 |
| 50% | 1275000 |
| 75% | 10000000 |
| max | 3151140000 |
Overall average funding raised is 23 million dollars. Minimum funding is just 569 dollars and maximum is 3 billion dollars.
Let’s find out the startups with the highest and least fundings.
Finding maximum funded company
# Maximum funding
startup_df[startup_df['funding_total_usd']==3151140000][['permalink', 'name', 'homepage_url', 'category_list', 'funding_total_usd', 'status', 'country_code', 'state_code', 'region']]
Output:
| permalink | name | homepage_url | category_list | funding_total_usd | Status | Country_Code | State_Code | Region |
|---|---|---|---|---|---|---|---|---|
| /organization/flipkart | Flipkart | http://www.flipkart.com | E-Commerce & Online Shopping | 3151140000 | operating | IND | 19 | Bangalore |
The highest funding amount is attributed to Flipkart, a well known e-commerce platform in the industry, aligning with its substantial financial requirements and prominence.
Finding least funded company
# Maximum funding
startup_df[startup_df['funding_total_usd']==569][['permalink', 'name', 'homepage_url', 'category_list', 'funding_total_usd', 'status', 'country_code', 'state_code', 'region']]
Output:
| permalink | name | homepage_url | category_list | funding_total_usd | Status | Country_Code | State_Code | Region |
|---|---|---|---|---|---|---|---|---|
| /organization/ruralserver | RuralServer | http://www.ruralserver.com | Cloud Computing & Cloud Data Services & Domains & In | 569 | operating | IND | 36 | New Delhi |
Rural Server despite being one of the least funded startups, intriguingly continues to operate successfully.
Visualising distribution of number of funding rounds
# Visualising the distribution of number of Funding Rounds
plt.figure(figsize=(12, 6))
bars= plt.bar(funding_round_counts.index, funding_round_counts.values, color='skyblue', edgecolor='black')
plt.xlabel('Number of Funding Rounds')
plt.ylabel('Count')
plt.title('Distribution of Number of Funding Rounds')
plt.grid(axis='y', linestyle='--', alpha=0.7)
# Set the x-axis ticks explicitly to ensure all values are visible
plt.xticks(funding_round_counts.index)
# Adding data labels (count values) to the bars
for bar, count in zip(bars, funding_round_counts):
plt.text(bar.get_x() + bar.get_width() / 2, bar.get_height() + 10, count, ha='center')
# bar.get_x() + bar.get_width() / 2: This part determines the x-coordinate where the data label will be placed.
# It calculates the center of the current bar by adding half of the bar's width to its starting x-coordinate.
# bar.get_height() + 10: This part determines the y-coordinate where the data label will be placed.
# It positions the label slightly above the top of the bar by adding 10 units to the bar's height.
# Display the plot
plt.show()
Above code gives us the below plot - which visualises our results!
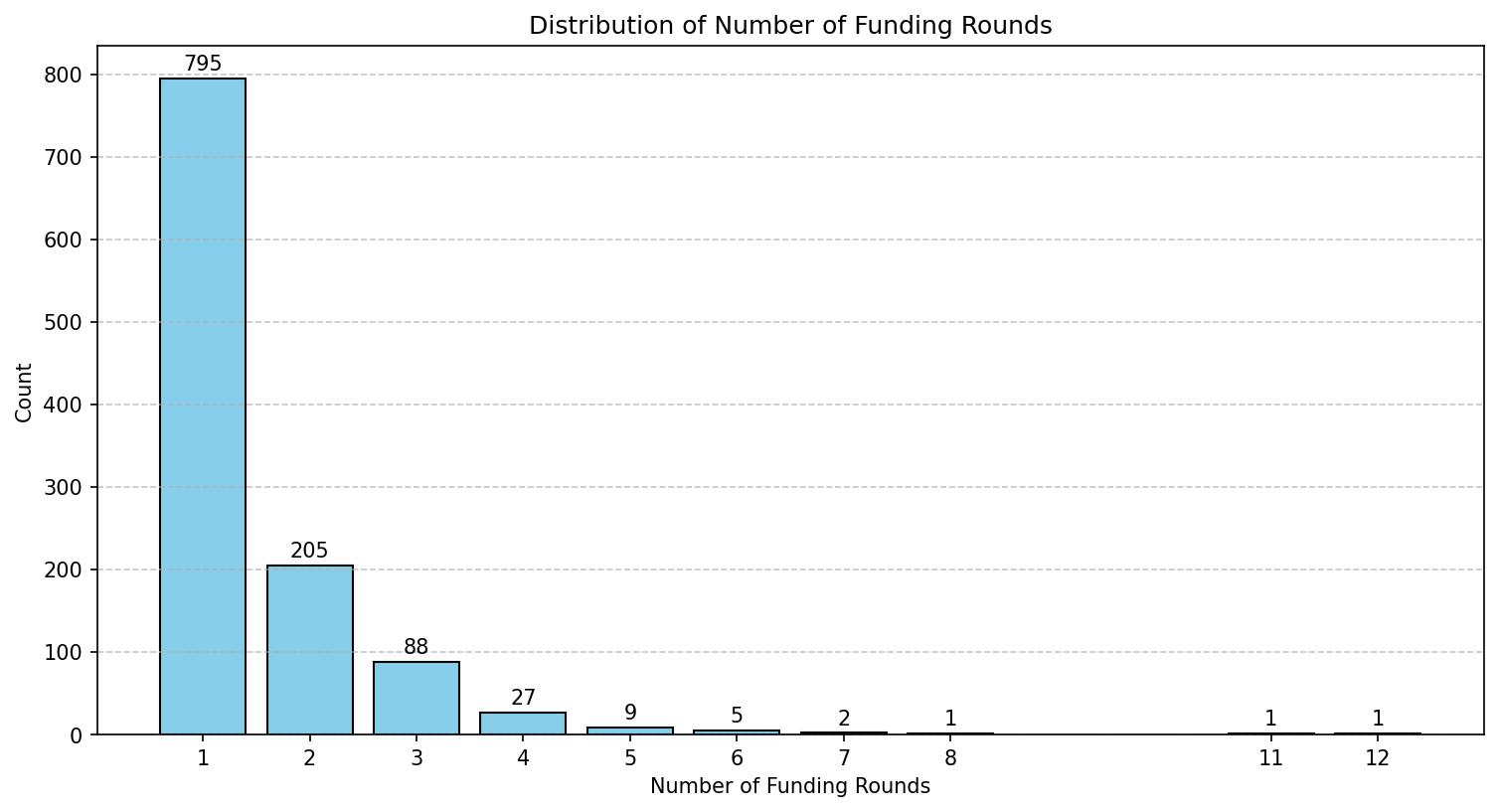
Remarkably, the majority of startups in our dataset, precisely 795 of them, have undergone just one round of funding. In stark contrast, only two startups have secured more than eight rounds of funding. Now, let’s delve into identifying these exceptional outliers within the dataset.
While running the hypothesis test we can create 3 categories for no. of funding rounds ~ 1, 2, 3+.
Checking company with 11 rounds of funding
startup_df[startup_df['funding_rounds']==11][['permalink', 'name', 'homepage_url', 'category_list', 'funding_total_usd', 'status', 'country_code', 'state_code', 'region']]
Output:
| permalink | name | homepage_url | category_list | funding_total_usd | Status | Country_Code | State_Code | Region |
|---|---|---|---|---|---|---|---|---|
| /organization/snapdeal | Snapdeal | http://www.snapdeal.com | E-Commerce | 1897699998 | operating | IND | 7 | New Delhi |
Checking company with 12 rounds of funding
startup_df[startup_df['funding_rounds']==12][['permalink', 'name', 'homepage_url', 'category_list', 'funding_total_usd', 'status', 'country_code', 'state_code', 'region']]
Output:
| permalink | name | homepage_url | category_list | funding_total_usd | Status | Country_Code | State_Code | Region |
|---|---|---|---|---|---|---|---|---|
| /organization/flipkart | Flipkart | http://www.flipkart.com | E-Commerce & Online Shopping | 3151140000 | operating | IND | 19 | Bangalore |
These represent some of the foremost e-commerce platforms, notably Snapdeal and Flipkart.
Now that we’ve gained a comprehensive understanding of the dataset, let’s proceed to test our hypothesis.
Applying Two Sample Independent T-Test
Using an Independent Sample T-Test in this context is justified for the following reasons:
-
Comparing Two Independent Groups: The independent sample t-test is suitable when we are comparing two separate and independent groups, which aligns perfectly with our scenario of comparing currently operating startups with startups that have closed. These two groups are distinct and unrelated in terms of their current status.
-
Continuous Numeric Data: The t-test is designed for comparing means of continuous numerical data, which is precisely what we have in our hypothesis testing. We are interested in comparing the mean funds raised, a continuous variable, between the two groups.
-
Normal Distribution Assumption: The t-test assumes that the data within each group follows a normal distribution. While this assumption should be checked, it often holds reasonably well for financial data, especially when the sample size is sufficiently large ~ we know basis EDA that both have >30 sample size
-
Homogeneity of Variance: We must check that using Levene Test.
The Levene’s Test is a statistical test used to assess whether the variances of two or more groups are equal or homogenous. It is particularly valuable when comparing multiple groups with the same independent variable to ensure that the assumption of homogeneity of variances, a key assumption in many statistical tests, is met.
In practical terms, Levene’s Test helps you determine whether it’s appropriate to use statistical tests that assume equal variances across groups, such as the independent sample t-test or analysis of variance (ANOVA). If the test indicates unequal variances, you may need to consider alternative statistical methods that are more robust to heteroscedasticity (unequal variances).
Overall, Levene’s Test is a valuable tool in the field of statistics for assessing the homogeneity of variances and ensuring the validity of subsequent statistical analyses.
Using Levene’s Test
null_hypothesis = "The null hypothesis in Levene's Test is that there are no significant differences in the variances of the groups being compared. In other words, it assumes that the variances are equal across all groups."
alternate_hypothesis = "The alternative hypothesis in Levene's Test is that there are significant differences in the variances of the groups being compared. If the p-value is sufficiently small, you would reject the null hypothesis in favor of the alternative, indicating that at least one group has a significantly different variance compared to the others."
alpha = 0.05
from scipy import stats
group1 = startup_df[startup_df['status'] == 'operating']['funding_total_usd']
group2 = startup_df[startup_df['status'] == 'closed']['funding_total_usd']
stat, p_value = stats.levene(group1, group2)
print(f"Levene's Test Statistic: {stat}")
>> Levene's Test Statistic: 0.36074537025282777
print(f"P-value: {p_value}")
>> P-value: 0.5482127964683872
# print the results (based upon p-value)
if p_value <= acceptance_criteria:
print(f"As our p-value of {p_value} is lower than our acceptance_criteria of {acceptance_criteria} - we reject the null hypothesis, and conclude that: {alternate_hypothesis}")
else:
print(f"As our p-value of {p_value} is higher than our acceptance_criteria of {acceptance_criteria} - we retain the null hypothesis, and conclude that: {null_hypothesis}")
>> As our p-value of 0.5482127964683872 is higher than our acceptance_criteria of 0.05 - we retain the null hypothesis, and conclude that: There is no significant differences in the variances of the groups being compared. They are equal.
We have determined that the variances are equal, thus meeting the assumption for the independent sample t-test. We can now proceed with the independent sample t-test confidently.
Undertaking Independent Two Sample T-Test - Mean Funds Raised
# Number of startups which are operating
startup_df[startup_df['status']=='operating']['funding_total_usd'].count()
>> 1085
# Number of startups which are closed
startup_df[startup_df['status']=='closed']['funding_total_usd'].count()
>> 49
# Create a new data frame of only those companies which are still operating and their respective funds
df1 = startup_df.loc[startup_df['status'] == 'operating', ['funding_total_usd']].reset_index(drop=True)
df1 = df1.rename(columns={'funding_total_usd':'Funds_operating'}).reset_index(drop=True)
df1.head()
Output:
| Funds_operating |
|---|
| 10000000 |
| 6369507 |
| 4000000 |
| 20000 |
| 2065000 |
df2 = startup_df.loc[startup_df['status']=='closed',['funding_total_usd']].reset_index(drop=True)
df2 = df2.rename(columns={'funding_total_usd':'Funds_closed'})
df2.head()
Output:
| Funds_closed |
|---|
| 25000 |
| 10000 |
| 10000000 |
| 40000 |
| 25000000 |
df2 = startup_df.loc[startup_df['status']=='closed',['funding_total_usd']].reset_index(drop=True)
df2 = df2.rename(columns={'funding_total_usd':'Funds_closed'})
df2.head()
Output:
| Funds_operating | Funds_closed |
|---|---|
| 10000000 | 25000 |
| 6369507 | 10000 |
| 4000000 | 10000000 |
| 20000 | 40000 |
| 2065000 | 25000000 |
# Funds_Sample1 represents funds for operating startup
# Mean funds (in million) for startup which are operating
mean_1=df3['Funds_operating'].mean()
print('Mean funds (in million) for startup which are operating is:',mean_1)
>> Mean funds (in million) for startup which are operating is: 23981373.343251728
# Funds_Sample2 represents funds for closed startup
# Mean funds (in million) for startup which are closed
mean_2=df3['Funds_closed'].mean()
print('Mean funds (in million) for startup which are closed is:',mean_2)
>> Mean funds (in million) for startup which are closed is: 10322911.346938776
null_hypothesis = "There is no statistically significant difference in the mean funds raised by currently operating startups and startups that have closed."
alternate_hypothesis = "There is a statistically significant difference in the mean funds raised by currently operating startups and startups that have closed."
alpha = 0.05
# Hypothesis Testing
t, pvalue = ttest_ind(df3['Funds_operating'], df3['Funds_closed'], nan_policy = 'omit')
# Print results
print('T-statistic:', t)
>> T-statistic: 0.6085283061630911
print('P-value:', pvalue)
>> P-value: 0.5429592211146083
# print the results (based upon p-value)
if p_value <= acceptance_criteria:
print(f"As our p-value of {p_value} is lower than our acceptance_criteria of {acceptance_criteria} - we reject the null hypothesis,
and conclude that: {alternate_hypothesis}")
else:
print(f"As our p-value of {p_value} is higher than our acceptance_criteria of {acceptance_criteria} - we retain the null hypothesis, and conclude that: {null_hypothesis}")
>> As our p-value of 0.5429592211146083 is higher than our acceptance_criteria of 0.05 - we retain the null hypothesis, and conclude that: There is no relationship between the mean funds raised by the two groups i.e. startups which are operating & startups. They are independent.
The p-value, which is greater than the chosen alpha level (i.e., 0.54 > 0.05), leads us to fail to reject the null hypothesis with 95% confidence.
As we can see from the output of these print statements, we do indeed retain the null hypothesis. We could not find enough evidence that funds raised between currently operating startups and closed startups were different - and thus conclude that there is no statistically significant difference in the funds raised between currently operating startups and closed startups.
Applying Chi-Square Test For Independence
The Chi-Square Test of Independence is typically used when you have categorical data and you want to investigate whether there is a statistically significant association or relationship between two categorical variables.
In our case, you are interested in the number of funding rounds (which is likely a discrete, count variable) and the status of startups (which is categorical - either “currently operating” or “closed”).
Here’s why the Chi-Square Test of Independence is suitable for our hypothesis.
We know that observations are independent, Cells in the contingency table are mutually exclusive, The only thing we need to check is if ~ Expected value of cells should be 5 or greater in at least 80% of cells.
Number of Funding Rounds
# Define a function to categorize funding rounds
def categorize_rounds(round):
if round == 1:
return '1'
elif round == 2:
return '2'
else:
return '3+'
# Apply the categorize_rounds function to create a new 'category' column
startup_df['rounds of funding category'] = startup_df['funding_rounds'].apply(categorize_rounds)
# Print the DataFrame with the new category column
startup_df[['permalink', 'name', 'homepage_url', 'category_list', 'funding_total_used', 'Status', 'Country_Code', 'rounds of funding category']]
Output:
| permalink | name | homepage_url | category_list | funding_total_usd | Status | Country_Code | rounds of funding category |
|---|---|---|---|---|---|---|---|
| /organization/-fame | #fame | http://livfame.com | Media | 10000000.0 | operating | IND | 1 |
| /organization/21diamonds-india | 21Diamonds | http://www.21diamonds.de | E-Commerce | 6369507.0 | operating | IND | 1 |
| /organization/247-learning-private | 24x7 Learning | http://www.24x7learning.com | EdTech Education Systems | 4000000.0 | operating | IND | 1 |
| /organization/33coupons | 33Coupons | http://33coupons.in | Internet | 20000.0 | operating | IND | 1 |
| /organization/3dsoc | 3DSoC | http://www.3dsoc.com | 3D Mobile | 2065000.0 | operating | IND | 2 |
Observed Frequencies
# Create cross tab
pd.crosstab(startup_df['rounds of funding category'], startup_df['status'])
Output:
| rounds of funding category | closed | operating |
|---|---|---|
| 1 | 39 | 756 |
| 2 | 7 | 198 |
| 3+ | 3 | 131 |
Expected Frequencies
contingency_table = pd.crosstab(startup_df['rounds of funding category'], startup_df['status'])
# Calculate expected frequencies
expected_frequencies = stats.contingency.expected_freq(contingency_table)
# Create a DataFrame to display the expected frequencies
expected_df = pd.DataFrame(expected_frequencies, columns=contingency_table.columns, index=contingency_table.index)
# Display the expected frequencies
print("Expected Frequencies:")
print(expected_df)
Output:
| rounds of funding category | closed | operating |
|---|---|---|
| 1 | 34 | 761 |
| 2 | 9 | 196 |
| 3+ | 6 | 128 |
All the values in the expected frequencies exceed the threshold of 5, indicating that our dataset meets the assumption of expected cell frequencies for the Chi-Square Test of Independence. Consequently, we are well-equipped to advance with our hypothesis testing.
null_hypothesis = "There is no statistically significant difference in the number of funding rounds between currently operating startups and startups that have closed."
alternate_hypothesis = "There is a statistically significant difference in the number of funding rounds between currently operating startups and startups that have closed"
alpha = 0.05
# Import library
from scipy.stats import chi2_contingency
# Run the Chi Square Test
chi2, pval, dof, exp_freq = chi2_contingency(contingency_table, correction = False)
print('The p-value is',pval)
>> p-value is 0.2908506204110049
# print the results (based upon p-value)
if p_value <= acceptance_criteria:
print(f"As our p-value of {p_value} is lower than our acceptance_criteria of {acceptance_criteria} - we reject the null hypothesis, and conclude that: {alternate_hypothesis}")
else:
print(f"As our p-value of {p_value} is higher than our acceptance_criteria of {acceptance_criteria} - we retain the null hypothesis, and conclude that: {null_hypothesis}")
>> As our p-value of 0.2908506204110049 is higher than our acceptance_criteria of 0.05 - we retain the null hypothesis, and conclude that: There is no relationship in the number of funding rounds between currently operating startups and startups that have closed. They are independent
The p-value, which is greater than the chosen alpha level (i.e., 0.29 > 0.05), leads us to fail to reject the null hypothesis with 95% confidence.
As we can see from the output of these print statements, we do indeed retain the null hypothesis. We could not find enough evidence that number of funding rounds between currently operating startups and startups that have closed were different - and thus conclude that there is no statistically significant difference in the number of funding rounds between currently operating startups and startups that have closed based on our dataset and chosen level of significance.
Conclusion
Based on the statistical analyses conducted, it can be concluded that:
-
There is no statistically significant difference in the funds raised by currently operating startups and startups that have closed, as per the independent sample t-test.
-
There is no statistically significant association between the number of funding rounds and the status of startups, as indicated by the Chi-Square Test of Independence.
Growth & Next Steps
Due to probabilistic nature of the hypothesis testing, Our results here also do not say that there definitely isn’t a difference in the mean funds/number of funding rounds between the two status groups aka ‘operating’ & ‘closed’ - we are only advising that we should not make any rigid conclusions at this point.
Running more tests like this, gathering more data, and then re-running this test may provide us, and the client more insight!